トップページ > 経済数学目次 > 最適化問題 1 2 3 4
5.多変数の場合の最適化問題
多変数の場合、偏微分、そして行列式の知識が必要になります。ぴーすけ講座では行列に関してはのちほど説明しますので、ここでは行列式を用いずに説明できる2変数までにとどめておきます。
2変数の場合の1階の条件はやはり接線の傾きが0になっていることです。しかし、1変数の場合と違って、2つ以上方向がありますので、x軸方向において接線の傾きが0、y軸方向において接線の傾きが0という条件が必要になります。つまり
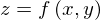
の1階の条件は
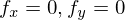
となります。少し言い換えてみましょう。1変数の場合、
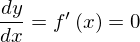
が1階の条件でした。これを書き換えると
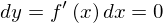
です。つまり、2変数の場合も1階の条件は
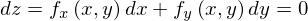
ということになります。dx,dyは変数と同じような扱いですから、これらが0になるという条件を課すことはできません。したがって、この式が0になるためにはdx,dyの係数が0にならなければなりません。したがって、
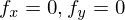
という条件が1階の条件になるのです。この規則性に従って2階の条件が導き出せます。ここでは極大値を例にしましょう。1変数の場合の2階の条件は
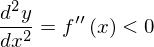
でした。つまり、
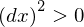
ですから
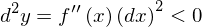
ということです。となると、2変数の場合の2階の条件も
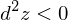
となればいいようです。そうとなると
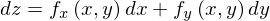
ですから、この式をもう一度全微分します。そうすると
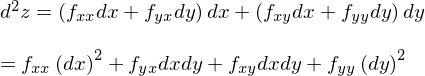
話を簡単にするためにヤングの定理が成り立つ場合のみを考えます。(つまりf(x,y)が2階連続微分可能と仮定します。)したがって、
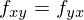
とします。したがって、2変数の場合の2階の条件は、
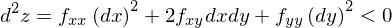
となります。この条件を2階偏微分係数の条件に書き換えるために、この式を平方完成します。
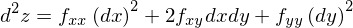
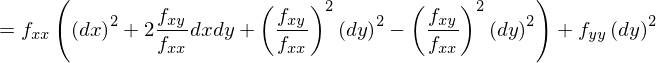
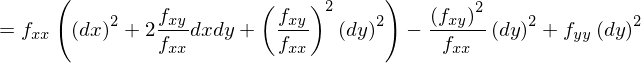
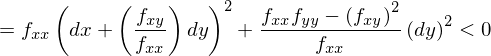
となりますから、不等式を満たすために、2階の偏微分係数は
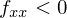
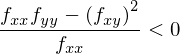
という条件を満たせば十分であるということになります。二つ目の条件は
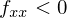
ですから、
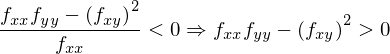
となります。行列式を知っている方であればヘッセ行列の行列式によって2階の条件が下のようにあらわせるということがわかると思います。ヘッセ行列は
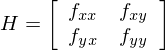
ですから、ヘッセの首座小行列式を用いて
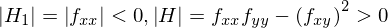
と2階の条件があらわせるということがわかります。(行列式がわからない人は読み飛ばしていただいて結構です。行列式を用いた2階の条件は中級編にて)では、2変数の場合の1階の条件、2階の条件をまとめると、
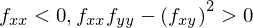
ということになります。これが極大値であることの十分条件であることの厳密な証明にはテーラー展開が必要ですので、中級編で説明します。これで、この章を終わりにします。

