トップページ > 経済数学目次 > 最適化問題 1 2 3 4
1.イントロダクション
経済学ではよく最適化問題を解きます。利潤を最大化するとか支出を最小化するなどなど、経済学部で学ぶ最適化は主に、静学最適化、静学条件付き最適化、動学最適化、条件付き動学最適化の4つです。条件のつかない動学最適化問題を解くことはないので、(少なくとも私の記憶にはありません。制約がなければ、静学最適化と変わらない解になるはずです。)条件付き動学最適化を動学最適化と呼びます。この章では最も基礎となる「最適化」について学びます。最適化とは目的関数を最大化または最小化することです。そして、最適化するために使う数学ツールは方程式を解く力と、「微分」だけなのです!
2.最大値、最小値の特徴
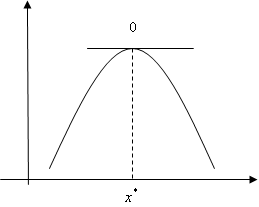
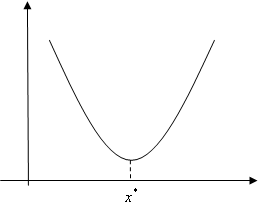
最大値、最小値の特徴を見てみましょう。右の図を見てください。
今、右の関数はx*で最大値をとっています。このx*は一つ特徴を持っています。それは関数の接線の傾きが0であるということです。(右の図をクリックしてください。)したがって、x*で最大値をとるならば
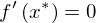
であると右の図では言えます。
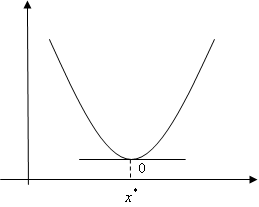
次に、右の図の関数はx*で最小値をとっています。ここでも同様に関数の接線の傾きが0であるという特徴を持っています。(右の図をクリックしてください)したがって、x*で最小値をとるならば
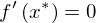
であると右の図では言えます。
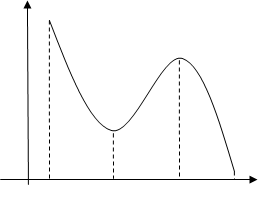
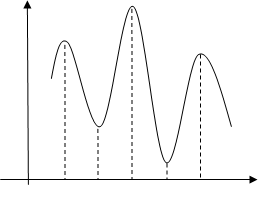
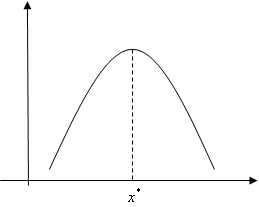
ここで、敢えて「右の図では言えます」と言っているのには二つ理由があります。一つは右の図のように最大値、最小値が端っこの点になっている場合があるためです。このとき、最大値または最小値ならば接線の傾きが0であるとは言えません。もうひとつは右の図(右下)のように接線の傾きが0になるという点がいくつもある場合があるからです。
となると、「最大値または最小値であるならば、それは端っこの点か接線の傾きが0になる点のいずれかの点である」ということが言えます。そこで端っこの点のことを端点と呼び、接線の傾きが0になる最大値(global maximum)の候補を極大値(local maximum, relative maximum)、最小値(global minimum)の候補を極小値(local maximum, relative maximum)と呼びます。そして、極大値と極小値を合わせて極値と呼びます。
したがって、最大値または最小値になるのは端点か極値であるということになります。しかし、端点が現れるのはxやyの範囲に制約がかかっている時のみです。例えば
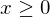
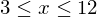
などです。端点の場合は上にあるようなxの端の値を代入して他の最大値や最小値の候補と比べるしかありません。したがって、ここでは極値に関してもっと詳しく議論します。(ちなみに有界かつ閉の連続関数であるときに最大値と最小値は存在します。有界じゃなかったり、xの範囲が開区間だったり、関数が連続じゃなかったりすると、最大値、最小値が存在しない場合があります。これを最大値・最小値の定理と言いますが、詳しい証明は中級編でします。)
ここで、例を挟んで、今まで学んだことのまとめと次の課題みつけましょう。例えば、ある企業の利潤Πが生産量Qによって決定され、利潤関数が
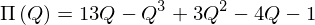
と表せるとします。このとき、利潤最大化する生産量を求めてみましょう。利潤関数を微分すると
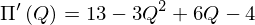
です。これが接線の傾きですから、これを0にするQを求めればいいのです。したがって、
"./mathequ/equmath86.png">
したがって、Q=3、Q=−1のどちらかで利潤を極大化し、どちらかで利潤を極小化しているということになります。尚、生産量は負の値をとれませんから、
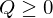
という制約がつきます。そして解答を先に答えると利潤を最大化する生産量は3ということになるのですが、Q=3、Q=−1のどちらが利潤を極小化しており、どちらが利潤を極大化しているという判断はどのようにしたらいいのかという疑問が残ります。また、Q=0も端点なので気になります。そこで、次のページでこのことについて言及します。