トップページ > 経済数学目次 > 条件付き最適化問題 1 2 3
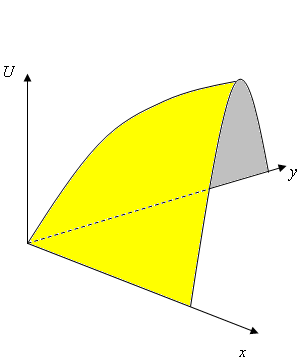
1.イントロダクション
前の章では、最適化問題を考えました。今度はそれに制約を設けます。たとえば
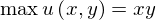
subject to 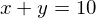
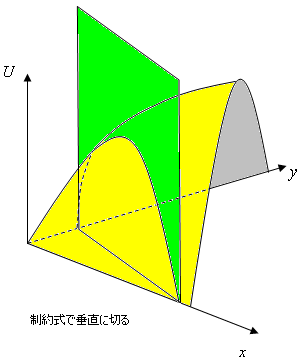
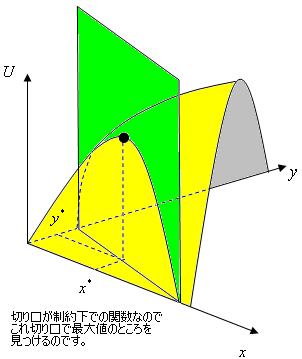
というような問題です。「subject to 〜」というのは「〜という制約のもとで」という意味です。学部レベルのミクロで最も多く解く最適化問題は条件付き最適化問題です。予算制約のもとでの効用最大化問題、資源制約のもとでの利潤最大化問題、生産量を所与としたときの費用最小化問題などです。これらは全て、条件付き最適化問題として解きます。上の問題を解くというのは、右の図のような点を求めることを示しています。(上の図を2回クリックしてください)(制約式の傾きが明らかに45度じゃないのは作画上うまくいかなかったのでどうか許してください。)
2.制約の種類
制約には主に2種類あります。ひとつは等式の制約、つまり
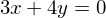
という風に=がある制約です。この制約が出てきた場合、ラグランジェ未定乗数法という方法で解きます。もうひとつの制約は不等式の制約、つまり、
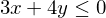
という風に≦、または≧のある制約のことです。強い不等式(<や>など=がない不等式)が制約式になることはありません。というか、強い不等式になると、その強い不等式が影響力をもった時点で最適値が存在しなくなるので扱えません。=も含めた不等式が条件になった場合、クーンタッカーの方法(クーンタッカーの条件)を使います。クーンタッカーもそんなに難しい話ではないのですが、この章ではラグランジェ未定乗数法のみを説明することにします。クーンタッカーは中級編で行います。
3.ラグランジェ未定乗数法
等式の制約付き最適化問題を解く場合、解き方は制約式を目的関数に代入することによる制約の内部化とラグランジェ未定乗数法の二種類方法があります。前者は制約式が少なく、代入しやすい場合、計算が楽になる場合があります。後者は制約式の数が多く、また、経済学的直観を得るために有用です。
初めに代入法を用いて、先ほどの例題を解いてみましょう。
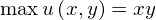
subject to 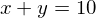
ですから、
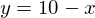
です。したがって、この式を目的関数に代入すると
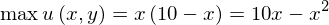
です。こうすると1変数の条件なし最適化問題と同じですからxで微分して0とおきます。
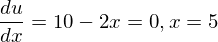
制約式に代入して、
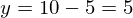
よって、制約のもとで、関数u(x,y)を最大化させるxとyは
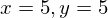
である。
(2解の条件が満たされているかどうかはみなさんチェックしてみてください。)この方法は条件付き最適化問題を条件なし最適化問題にしてから解くという方法ですね。しかし、制約式が代入できる形になるという保証もありませんし、制約式がたくさんでてきたら、全ての制約式を目的関数に代入するのはむしろ時間がかかります。そこで、(ここではあまり有難味を感じないかもしれませんが、)ラグランジェ未定乗数法を用いて先ほどの例題を解いてみましょう。(なぜ、この方法で解が求まるかは後述します。)