トップページ > 経済数学目次 > 指数・対数の微分入門 1 2 3
1.イントロダクション
ここでは前回の微分の話に続いて、logと指数関数の微分、そして最後によく使う微分の公式(前章での微分の公式1)の証明を行います。指数関数の微分は連続時間を扱う時に必要になります。対数の微分は、効用関数、生産関数においてよく対数表示が扱われるため必要になります。効用関数とか対数をとって単調変換したりもしますから。それでは、まず対数関数(log)の微分の証明から行いましょう。
2.対数の微分
対数関数を微分すると
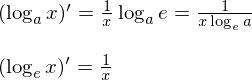
となります。ただし、
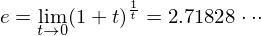
です。それでは、これについて証明しましょう!「である調」でいきます!
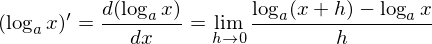
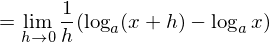
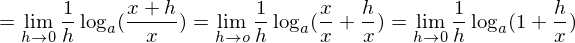
(この上の式展開がわからない方は経済数学対数の計算へ。)ここで式の変形を理解しやすくするために
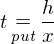
とおく。そこで二つことに留意する。
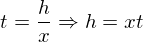
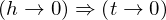
(一つ目はただの式変換、二つ目はhが0に近づくならばtも0に近づくという意味です。)
そこでさっきの対数の微分の式の続きに一つ目の式に代入すると
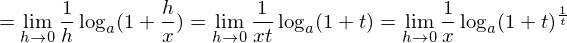
ここでhが消えたので、二つ目の式よりlimをh→0からt→0に置き換える。よって
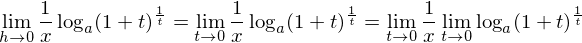
1/xはtに関係ないので、lim(1/x)=1/xである。問題はログの中にlimが入ることができるのか、ということであるが、これはlogが連続関数であるためにlimが中に入ることができるのである。(中級編で証明します。)したがって、
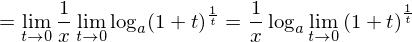
そして最後の問題として
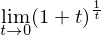
はどのような値になるのか?ということがある。()の中は1に近づくが、累乗は無限大になる。1なら何乗しても1だが、1より少しでも大きければ無限大の累乗によって発散してしまう。そこで具体的な数字をtに入れて0に近づけていってみたいと思う。
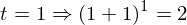
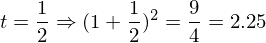
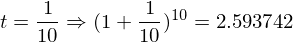
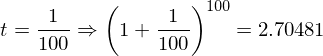
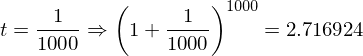
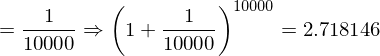
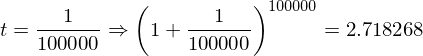
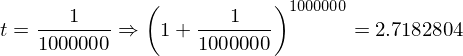
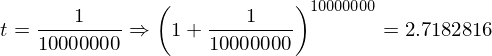
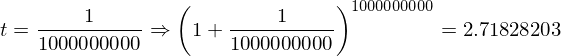
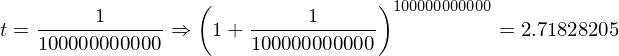
だいたい2.71828…くらいの値になりそうだ。(きちんとした証明は中級編で行います。)これは無理数(分数で表せない数)で円周率が3.14159265358…と続いたようなものである。それでこの2.71828…=eとおく。円周率が3.14159265358…=πであるように。それで
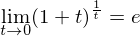
となり、これで、対数の微分が完成する。
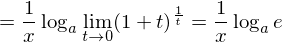
したがって
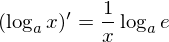
となる。また、対数の底の変換公式(わからない方はここへ)より底をeに変換すると
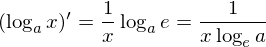
が得られる。また、a=eの特殊なとき
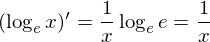
である。証明終了。
eはネイピア数と呼ばれ、経済学では他にも連続時間における「時間選好率」や「利子率」においてよくつかわれます。また、底がeの対数を「自然対数」とよびます。自然対数は微分後の形がきれいなので、底が10である常用対数と同様によく使われます。経済学では常用対数よりも自然対数をよく用います。そしてよく使われるものは、省略されます。したがって、
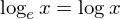
とすることが多々あります。経済学では底が省略されているとき、どこかで断りがない限りeが底となっています。しかしこれでは常用対数と間違える場合があるので
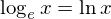
と表記されることの方が多々あります。lnは自然対数(natural logarithm)の省略です。では次のページでは指数関数の微分、微分の公式1の証明を先に行い、その次のページで計算例をだします。

