トップページ > 経済数学目次 > 指数・対数の微分入門 1 2 3
３．指数の微分
この節では指数の微分の証明行います。指数関数の微分の公式を表すと、
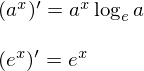
です。ただし、eはネイピアの数です。さて証明に移ります。ここでも同様に「である調」を用います。
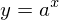
とする。両辺に自然対数をとると
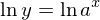
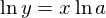
両辺をxで微分する。chain ruleより左辺は
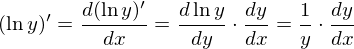
右辺では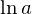
が定数であるので
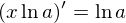
である。したがって、
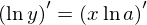
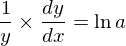
今はdy/dxを求めたいので
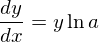
また、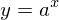
なので代入すると
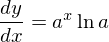
特にa=eのとき、
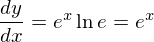
となる。これにより指数関数の導関数が求められた。証明終了。
このようにして、対数をとって微分をすることで証明する方法を対数微分法といいます。ネイピアの数を底とする指数関数（指数関数の底とは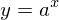のaのことです。）なんてもともとの関数と導関数が変わらないですからね。不思議です。微分しても形が変わらない関数ですから。つまり、関数のいたるところで関数値と接線の傾きが等しいということです。では次に微分の公式１も対数微分法を使って証明しましょう！
４．微分の公式１の証明
まぁ、私が微分の公式１って名前をつけておきながら、２はないんですけどね。何か特殊な名前があるといいんですけど。。。では、微分の公式１の証明を行います。微分の公式１は
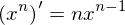
でしたね。それでは「である調」で証明します。
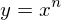
とする。両辺に自然対数をとると
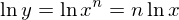
両辺をxで微分する。chain ruleより左辺は
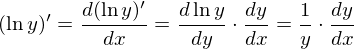
となり、右辺をxで微分すると、
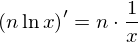
となる。したがって、
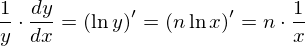
となる。求めたいのはdy/dxなので
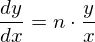
ところで
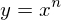
なので、代入すると
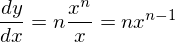
となる。したがって、微分の公式１が導かれた。証明終了。
このようにして、初めに用いていた微分公式１が求められます。ちなみに微分の公式１を二項定理や積の微分の公式を用いて証明するのがありますが、二項定理を用いるとnが自然数に限られるためnが自然数のときのみの証明になりますし、積の微分の公式を用いた場合はnが有理数の場合までしか証明できません。ですが、この証明はnに特に制約を設けていないのでnが「実数」の場合において微分の公式１が成り立つことを証明していることになります。つまり、nが無理数でもいいのです。たとえば
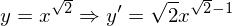
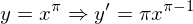
ということです。では、次のページで対数関数の微分と指数関数の微分の例をだして終わりにしたいと思います。