1.イントロダクション
前章では偏微分を学びました。偏微分は他の変数を一定として、ある1変数だけを動かした時の微分でした。でしたから、1変数の場合の微分とそれほど変わりなくできました。ここでは、先ほどとは反対にすべての変数を動かします。そのため、1変数の場合とはいろいろと異なる場合がでてきます。この章ではまず、全ての変数を動かすと何が問題なのかを説明し、直感的に全微分を説明した後、理論的に全微分を説明していきます。
2.多変数と1変数の違い
多変数関数と1変数関数の違いは前の章で説明しましたが、「多変数と1変数の違い」については説明していませんでした。この節ではそれらの違いの全てを説明するわけではありませんが、全微分をするうえで問題となる違いを説明します。
1変数の微分の定義式では がでてきました。これはxの差分で、点xからの変化分を表しています。これは点xからの距離のみを表していました。たとえば、
今、家から100mの地点にいます。家から100m離れました。家から何mの地点にいますか?
と問われれば200mと簡単に答えられます。だって100+100ですから。

また、上の図のように家への帰り方(家への近づき方)も一つしかありません。(もうひとつ考えるなら、家をいったん通り過ぎて、左から近づくことですね。)
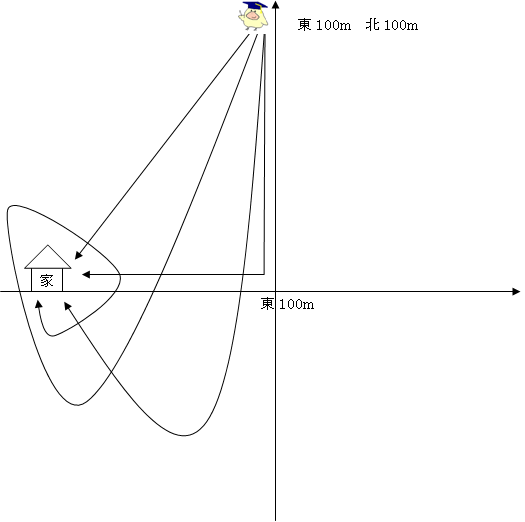
しかし、変数が二つになると話は変わります。家から東に100mいる場所から北に100m移動しました。家から何mの場所にいるでしょうか?
これは簡単に100+100=200mというわけにはいかなくなりました。図で書くと中学3年生で習った三平方の定理から
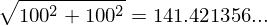
だいたい家から141mの場所にいます。(これを2次元のユークリッド距離といいます。詳しくは中級編で。)なぜ、さきほどと同じように足し合わせてはいけないのでしょうか?1変数と2変数の大きな違いは何でしょうか?それは「向き」です。1変数では+と−しかありませんから、数字の「大きさ」のみを考えればよかったのです。しかし、2変数以上になると「大きさ」と共に「方向(向き)」ということを考えなければならないのです。同じ100m(大きさ)でも、北に進むのか東に進むのか北東に進むのか(方向)で足し合わせ方が変わってきます。これは別に距離にのみ言えることではなく、変数が2種類以上組み合わせると、距離と同様に「方向」が現れるのです。そこで、それら数字の組み合わせを数字が1つの場合と対比してベクトルと呼んだのです。ちなみにひとつの数字である場合をスカラーと呼ぶことにしました。(英語で発音するとスカラーよりもスケイラーの方が近い音です。スカラーっていうと学者だと思われます。)ベクトルの詳しい話は中級編の行列でします。このように「スカラー」ではなく「ベクトル」となってしまうと、1変数で学んだ微分だけでは語れない部分がでてきてしまうのです。
また、方向が加わってしまったために下の図のように家への近付き方も何通りもでてきます。家の周り360度からどのような近付き方もしてもいいのです。これもまた、1変数のときよりも複雑になってしまいますね。これらが「全微分をするうえで問題となる違い」です。