3.全微分の直感的理解
さて、まず、厳密さを無視して全微分の直感的理解のための説明をします。1変数の微分、2変数の偏微分の定義式をみると
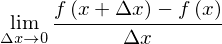
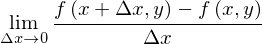
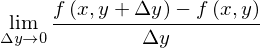
というものでした。これらが「1変数だけを動かした」のだとすれば「全ての変数を動かしたもの」は
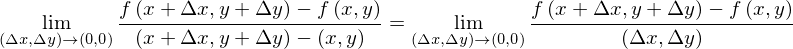
と書きたいところですが、これでは駄目なのです。分子はまだいいのです。なぜなら、スカラーですし、引き算は容易にできます。しかし、分母を見てください。分母がベクトルになっているのです。これが問題となる要因です。なぜならば、ベクトルの割り算は定義されていないからです。たとえば割る数がスカラーならば、東に2mを2で割ったなら東に1mという風に計算できますが、割る数がベクトルの場合、東に2mを北東3mで割りなさいと言われても意味がわかりません。東を北東で割るというのはどのようなことなのでしょう?このようにベクトルの割り算はできないのです。
そこで、次に考えるのは分母を距離にしてみてはどうだろうということです。つまり
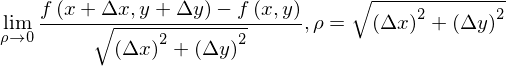
です。ちなみにρはローと呼びます。しかし、これでも駄目なのです。なぜかというと、これでは近づき方に方向が入っていないのです。前節において2変数ならば、家への近づき方も360度どの方向であってもいいと言いました。そのため、上記の式の極限値が存在したとしてもある特別な経路でのみ存在したにすぎません。例えるならばこうです。1変数において「微分可能である」とは「関数のグラフがなめらかなこと」と説明しました。2変数においても同様で、点(x,y)において微分可能であるとは、点(x,y)の周りでグラフがなめらかなのです。前のページの図において、「家」の場所が微分可能ならば、家の周りでなめらかな地形なのです。崖や階段、段差があってはいけません。家に東から近付けばなめらかだけども、西から近づいたら崖があった、となれば西から家には入れませんね。単に家からの距離を0に近づけるだけでは、とりあえず、家に近づいてみた。偶然、東から家に近づいたらなめらかに近づけた。西から近づいた場合はわかりません。ということなのです。したがって、あらゆる方向から近づいてもなめらかであるというには分母とlimの下を距離にしては駄目なのかもしれません。
それでは、limの下を距離のρではなく、方向を考えた(Δx,Δy)にしてみましょう。つまり、距離のみを0に近づけるのではなく、あらゆる方向も考慮して0に近づけるのです。つまり、
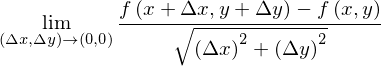
とするのです。だいぶ正解に近づいてきました。でも、まだ問題があるのです。それはこれが「傾き」になっているということです。一次元の時は右から近づいても、左から近づいても傾きは一致しました。そして一致することが微分可能の定義と一緒です。しかし、二次元となるとどうでしょう。東から近づいたとき、北から近づいたとき、北東から近づいたとき、傾きが必ずしも一致するでしょうか?いいえ。一般的には一致しないのです。となると、この「傾きの形」で微分を表すことをあきらめなければならないのです。
しかし、これではどうしたらよいのでしょうか。全微分した後の関数の形も見当もつきません。とりあえず、「傾き」表記である限りどうしようもなさそうです。そこで左辺の分母の二変数を、右辺にもってくればいいということに気づきます。そのため、まず1変数において分数の形であらわさない微分可能を考えてみましょう!ということになるのです。つまり、微分可能であるということの必要十分条件を考えるのです。では、1変数の場合を少し振り返りましょう。
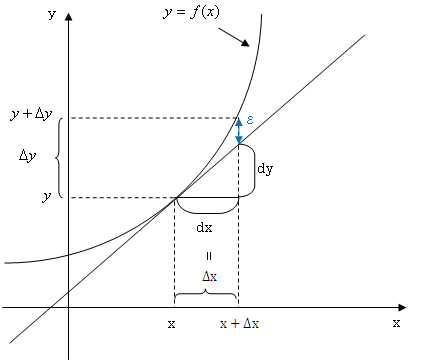
1変数の微分の定義式は
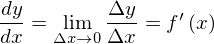
でした。まず、式変形するために極限limを外さなければなりません。さて、右の図のように誤差εがありました。この誤差を考慮すれば、Δxが0に十分に近くなくても等式が成り立ちます。そこで
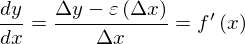
ただし、
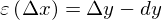
です。誤差がΔxの関数になっているのは、誤差がΔxによって変化するからです。そこで、式変形すると
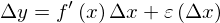
とすることができます。さて、分数を使わずに表せることができましたが、この式で「微分可能」を語るにはどうしたらいいのでしょうか?そこで右上の図をよく観察してみます。微分可能であるというのは「誤差εがΔxが0に近づくにつれて、0に近づけばいい」としていましたが、一つ見落としていたものがありました。誤差εが0に近づくよりもはやくΔxが0に近づいてしまったら、Δxが0に十分に近くても、εが0に十分近くないことがある、つまり誤差が無視できないじゃないか!?ということです。つまり、微分可能であるためには、Δxが0に近づくよりもはやく誤差εが0に近づかなければならないのです。そこでΔx→0のときεがΔxよりもはやく0に近づくというのはどのように式で表せるのでしょうか。それは
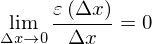
とあらわせます。分子の方が分母より0に近づくのがはやければ0になりますよね。もしもεよりもΔxがはやく0に近づくとなると上の式の値は∞になります。
(一般的にα→0のとき、β→0であり、α→0のとき、(β/α)→0ならば、βをαの微小数といいます。)
したがって、微分可能であるというのは、
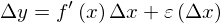
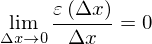
と書きかえられるのです。(証明は次の節でします。)ちなみにこれらのことを踏まえて、この式をみると、微分の新たなインプリケーションが得られます。微分可能ならば、Δxが0に近づくとき、f’(x)Δxとεが0に近づきますが、εが一層はやく0に近づくということがわかります。つまりそれは、Δyの主要部分がf’(x)Δxであるということを意味しています。この主要部分を微分とよび,dyとしたのです。したがって、
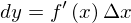
です。ところで、x=xという式は常に成り立っています。したがって、この式をxで微分すると
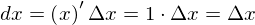
となり、
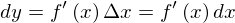
となるのです。
さて、分数を使わずに微分可能を表現できました。それでは、これを2変数に拡張してみましょう。

