トップページ > 経済数学目次 > 陰関数の定理入門 1 2 3
3.陰関数はたくさんある!?かも
さて、陰関数が実は陰関数は何かがわかったところで、ひとつ問題があります。陰関数って沢山あるかもしれないんですよ。言い換えれば、関数Fが
というxとyの関係fは沢山つくることができてしまうのかもしれないのです。
よくある例が
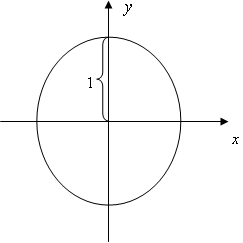
です。この式は右の図のような半径を1とする円の方程式です。そうするとxが決まるとyが2箇所決まってしまいますよね?(右の図を3回クリックしてください。)式をyについて解いても
となるわけですから、xが一つに決まっても
と
の二つが決まってしまいます。xが一か所決まったときにyが2箇所決まる場合は「関数」ではありません。関数はxが一か所決まったときにyが1箇所に決まる必要性がありますから。
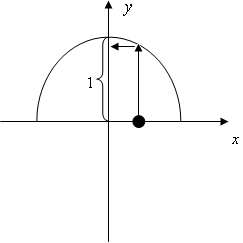
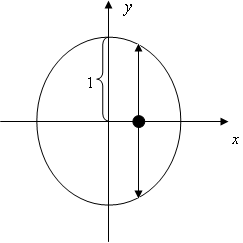
そこで、「じゃあxが決まった時のyの値が+にします」というルールを決めれば
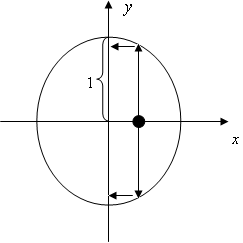
というxとyの関係(関数f)が右の図のように決まるのです。逆に、「xが決まった時のyの値は−にします」というルールをきめれば
と、さきほどとは違うxとyの関係(関数fとは異なる関数g)決まります。(右の図をクリックしてください)
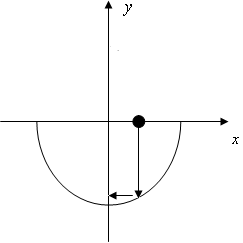
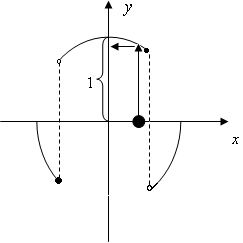
もっと自由度を上げて、
のときにyは−、
のときにyは+、
のときにはyは−と決めれば
という風にさらに異なるxとyの関係(関数fとも関数gとも異なる関数z)が決まります。(上の図をクリックしてください)したがって、
を満たすxとyの関係(陰関数)はいくらでも作り上げることが可能なのです。しかもが連続微分可能(微分可能でかつ微分した関数(1階の導関数)が連続である)でも陰関数が連続じゃない場合がありうるわけです。となると、少し困りましたね。関数が唯一に決まった方が、いろいろと便利ですし(無差別曲線が何本も見つかると不便ですし)、陰関数が微分可能じゃないと無差別曲線のMRSが導き出せないじゃないですか。さっきはyが+か-かということで関数を唯一に絞ってみましたけど、違う方程式ではyが+のときにも関数が二つ以上決まる場合(たとえばさきほどの円の方程式をy軸方向に1ずらすとか)だってあるでしょうから、先ほどの方法は陰関数を唯一みつける万能の方法ではありません。じゃあ、陰関数が唯一にきまり、陰関数が微分可能になる方法(つまりどんな連続微分可能な効用関数でも連続微分可能な無差別曲線を唯一に見つけられる方法)を考えましょう。