トップページ > ミクロ経済学目次 > 労働供給 1 2 3
3.労働供給の図による分析 続き
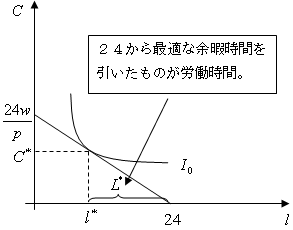
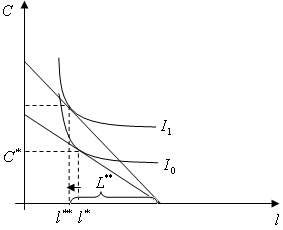
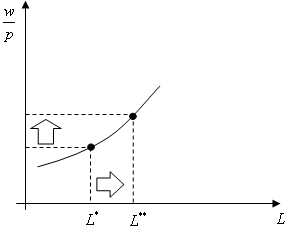
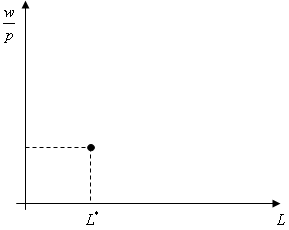
さて、労働供給曲線とさきほどの図の関係を図示しましょう。労働供給曲線は縦軸に実質賃金、横軸に労働供給量をとった平面に描かれます。現在、ある実質賃金のもとで右の図のように最適点が与えられたとします。そうすると、右下の図のように、実質賃金と労働供給の関係を表す1点が決まるのです。さて、ここで実質賃金を上昇させてみましょう。つまり、傾きがより急になるわけです。(右の図をクリックしてください)そうすると、右の図のように最適点が移動します。右の図の場合は、実質賃金の上昇によって労働供給量が増加したことになります。これを右下の図で表すと、実質賃金の上昇によって労働供給量が増加しているわけですから、さきほどの点よりも右上に点が移動するわけです。
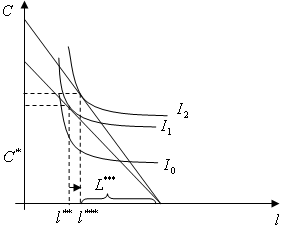
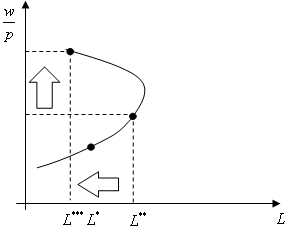
このように、賃金と労働供給量の関係を(連続的に)描けば、右下のように右上がりの労働供給曲線が描けるのです。通常はどんな実質賃金水準でもこのような右上がりの労働供給曲線を仮定することがよくあります。しかし、前のページで説明したように、実質賃金の上昇が必ずしも労働供給量を増加させるとは限りません。そして、経済学において、実質賃金の上昇が労働供給量を減少させる効果がある場合は十分に高い実質賃金のときに生じるとするのが通常です。それは決して直感からずれたものではありませんね。現在の賃金で十分に豊かな生活を送れている場合、さらに賃金が上昇すれば、消費水準の増加よりも、自分の時間を優先するはずである、ということです。(右の図をクリックしてください)したがって、更に賃金が上昇した場合を考えましょう。右上の図のように実質賃金の上昇によって最適点が、労働供給量を減少させるように決まるとします。そうすると、右上の下の図のように新たな実質賃金と労働供給量の関係は先ほどの点よりも左上に移動します。
そのとき、図のように労働供給曲線は単なる右上がり型ではなく、後方屈折(バックワードベンディング)型労働供給曲線になるのです。(右上の図をクリックしてください)この労働供給曲線に関しては、
屈折する前は「代替効果>所得効果」
屈折した後は「代替効果<所得効果」
ちょうど屈折しているところでは「代替効果=所得効果」
が満たされているということになります。ちなみに右上がり型労働供給曲線では常に「代替効果>所得効果」が満たされているということでもありますよ。
労働供給曲線の図と制約式&無差別曲線の図の関係性に関しては以上です。次に計算練習を行いましょう。
4.具体的な計算例
労働供給の計算問題をします。まず、1ページ目でも説明しましたように
という風に定式化ができます。ちなみにここではわかりやすくするために、時間制約として24という数値を用いましたが、24と特定化せず、Hと記号で計算する場合もあります。(1日において24時間が利用可能な最大時間であるというのは、確かなことですが、1日ではなく、1週間の労働供給量を求める問題にしてもいいですし、1日において学業の時間を差し引いた時間を用いて分析してもいいわけですし、いろいろなことへの応用を考えると、24という数値ではなく、Hという文字(定数、パラメータ)として分析したほうがいいということです。)
さて、問題を具体的に計算する練習のページですので、効用関数に具体的な形を入れてみましょう。まず、初めにコブ=ダグラス型効用関数の場合、つまり、
の場合を考えます。問題は最適消費量を解いたときと同じようにラグランジェ関数を用いて解きます。(ラグランジェ未定乗数法がわからない方はぴーすけ講座経済数学の制約付き最適化問題へ。指数計算がわからない人もぴーすけ講座の指数計算へ。)計算例は効用最大化問題でも経済数学の制約付き最大化問題でも紹介していますので、ある程度計算過程を省略します。
とラグランジェ関数をset upします。ただし、λは正のラグランジェ乗数です。したがって、一階の条件を導き出すと
となる。一つ目と二つ目の式をそれぞれ移項して比をとると
となる。(λは約分できるので、この式は限界効用の比(つまり限界代替率)が実質賃金と等しくなっているという条件です。)更に整理すると
となる。これを制約式に代入すると
つまり、最適な余暇水準は12である。したがって、最適な労働時間は
であるから、12である。また、消費水準は
である。計算終了。この問題の驚くべきことは、余暇水準と労働時間がいかなる実質賃金においても12であるということである。たとえば、この効用関数をもつ人は時給がいくらでも、物価水準が変動しても、必ず1日に12時間働く人なのです。これは、このコブ=ダグラス型効用関数だと、所得効果と代替効果の大きさが等しいと特性をもつためなのです。このことについての詳しい分析はスルツキー方程式の章で行いましょう。
さて、労働時間がさきほどの問題のように定数の値で求まると、「この式が労働供給関数なのです」といっても納得がいきづらいと思いますので、労働時間がきちんと実質賃金の変化によって、変化する場合の問題も解きましょう。
次の効用関数は
とします。先ほどと同様にラグランジェ関数を
とset upし、一階の条件を求めると
となる。一つ目の式と二つ目の式を移項し、比をとると
となり、
と求まる。これを制約式に代入すると
整理すると
と、最適な余暇水準が求まり、したがって、最適な労働供給量は
ともとまる。このように、最適な労働供給量を実質賃金の式で表したものを「労働供給関数」と呼びます。ちなみに、さっきコブ=ダグラス型効用関数で求めた最適労働供給量も式に実質賃金が表れていませんが、労働供給関数です。あの式は「実質賃金が労働供給に影響を与えない」ということを表していますから。さて、上の労働供給関数をいろいろな式で表していますが、ちょっと意味があります。一番右の式から、実質賃金の上昇が分母を小さくするため、労働供給量が増加するのがわかります。また、実質賃金を無限大に飛ばすと、分母の値が1に近づくため、最適な労働供給量が24に限りなく近づいていくのもわかります。つまり、この労働供給関数は単調増加で、上限が24なのです。右から2番目の式は式としてきれいです。右から3番目は実質賃金の式で表しているという条件のもとでは一番きれいです。(と、私は思います。)単調増加かどうかは、一階微分してもとめてもいいですね。上限が24であることをイプシロン=デルタ論法で求めるのは面倒ですね(笑)
ちなみに、最適な消費水準は
と求まります。右の式から見てとれるように、実質賃金の上昇が分母を小さくし、分子を大きくするわけですから、単調増加です。実質賃金を無限大に飛ばすと、分母は1に収束し、分子は発散しますから、消費水準に上限はありません。
この問題での労働供給関数は、右上がりの労働供給曲線ということですね。
バックワードベンディング型の労働供給曲線を描ける労働供給関数を効用関数の最適化問題から導出させるような問題を、私はまだ見たことがないので(先輩は自分たちで一体どんな効用関数なんだ!って言って自分たちで作り上げていましたが)ここでの例題としては扱いません。これで、この章を終りにしたいと思います。