トップページ > ミクロ経済学目次 > 効用最大化問題 1 2 3 4 5 6 7
代替の弾力性
代替の弾力性とは
と定義されます。最適条件を満たす場合
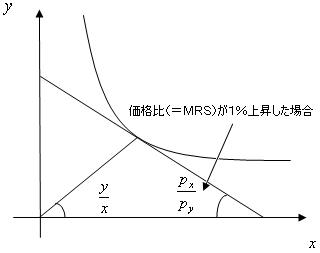
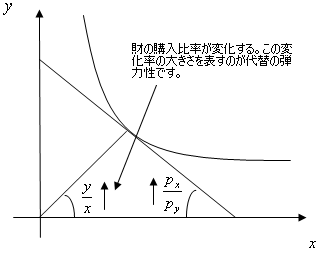
ですから、代替の弾力性のイメージは、価格比が1%変化した場合、財の消費する比率が何%変化するのかということを表しています。つまり、価格比が1%変化した場合、財をどれくらい代替するのかということを表しているのです。(上の図を2回クリックしてください)それでは、代表的な効用関数の代替の弾力性を計算してみましょう。
先ほどの式を直接計算すると結構手間がかかるので、少し変形します。それは
ですから、
と変形するのです。つまり、ln xの微分は微小の変化率と等しいわけですね。(厳密な証明には陰関数の定理を使ったほうがいいです。)したがって、先ほどの定義式を
と変形できます。それでは計算しましょう。
コブ=ダグラス型効用関数の場合
ですから、したがって、
したがって、
よって
です。つまり、コブ=ダグラス型効用関数の代替の弾力性は1になるのです。(逆関数の微分ができる人はそれを行ったほうが早いです。)
コブ=ダグラス型効用関数の場合代替の弾力性は定数になりましたが、必ずしも定数になるとは限りません。例えば
の場合
つまり、
となります。通常、このように変数に依存した形になります。
他にも代替の弾力性が定数になる効用関数があります。それは線形の効用関数とレオンチェフ型の効用関数です。(効用関数の場合、代替の弾力性が∞になるので、定数というと語弊があるかもしれません。)レオンチェフ型の場合、0となります。計算はウェブ閲覧者におまかせしますね。
さて、先ほど述べたように、代替の弾力性が定数になる効用関数とならない効用関数があることがわかりました。そこで、代替の弾力性が定数となる代表的な関数、CES関数(Constant Elasticity of Substitution function)があるのです。(読み方はシーイーエス関数と読む人もセス関数と読む人もいます。)CES関数は
とあらわせます。ただし、α、β、ρはパラメータで、特にρは1以下の値をとります。
さて、代替の弾力性を計算してみると、
となります。したがって、
となります。したがって、CES関数の代替の弾力性は
となるのです。きちんと定数になっていますね。
このCES関数はρの値によって、先ほど代替の弾力性が一定であると説明した、線形の関数にも、コブ=ダグラス型関数にも、また、レオンチェフ型関数にもなるのです。
ρ→1のとき、線形の関数に、ρ→−∞のとき、レオンチェフ型関数に、ρ→0のとき、コブ=ダグラス型関数になるのです。証明はCES関数についての章で。
それでは、この章を終りにします。
※コブ=ダグラス型関数の指数の和が1になるという定義となる必要はないという定義があります。つまり、α+β=1となる必要があるのか、ないのかということですね。そこで、使い分けるときには、α+β=1となるコブ=ダグラス型関数を「狭義のコブ=ダグラス型関数」、α+β=1という制約がないコブ=ダグラス型関数を「広義のコブ=ダグラス型関数」と呼びます。