トップページ > ミクロ経済学目次 > 効用最大化問題 1 2 3 4 5 6 7
いろいろな例題
次に
という効用関数を考えましょう。これはmin関数といって、最小化とは違います。よく見ると、minの次に{}といういつもと違う括弧がでてきていて、また、括弧のなかに , があります。min関数の意味は、{}の中の小さい方の値をとりなさい、という関数です。たとえば
という感じです。このmin関数を用いた効用関数をレオンチェフ型効用関数と呼びます。この効用関数をもつ人は、片方の財がいくら増えても、もう片方の財が増えなければ意味がないのです。みなさん、何かしらで片方しかなくて困ったことがありませんか?片方のみだと意味がない財の組み合わせのときレオンチェフ型効用関数になります。たとえば、右足用のスリッパxと左足用のスリッパy、片方だけあっても意味がないですね。両方あって初めて意味がありますね。このとき、
となるわけです。これはxとyが完全に補完されている財です。したがって、レオンチェフ型効用関数であらわせる財の組み合わせを完全補完財と呼びます。
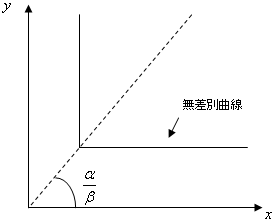
レオンチェフ型効用関数を図で表すと右の図のようになります。原点を通る傾きが(α/β)の直線上で90度に曲がります。この形状の説明はα=βのときが一番わかりやすいでしょう。α=βのとき、45度線上で無差別曲線が90度に曲がります。それはxとyが同じ数量のときを表しています。ところで、片方の財が増加するということはx軸またはy軸に平行に増加するということです。つまり、同じ数量のときから、片方の財だけ増えても同じ無差別曲線上にいるのですから、片方の財だけ増えても効用は増えないのです。これは先ほどのmin関数と同じ話ですよね。だから、レオンチェフ型の効用関数の無差別曲線はこのような形状になるのです。さて、それでは、最適化問題を解いてみましょう。
つまり、
subject to
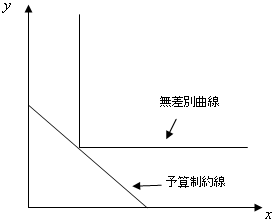
という問題です。厳密に解いてもいいのですが、ここでも図によるアプローチをしましょう。
右の図のように90度で曲がっている点で予算制約線と接しています。したがって、その接している点が最適点となります。しかし、90度で曲がっているため、微分可能ではありません。そのためラグランジェ未定乗数法で解くことができないのです。
しかし、解くのは簡単です。
90度に曲がっている点では
となっています。これが最適なxとyの組み合わせ方です。これを予算制約式に代入し
これをまた最適な組み合わせを表す式に代入すると
となるのです。
線形も効用関数だったら、無差別曲線の傾きと予算制約線の傾きによって場合わけをしながら端点解をもとめる。レオンチェフ型だったら、min関数の中身を=とおいて予算制約線と連立方程式を立てて解くというだけです。では、最後に次のページでCES関数と代替の弾力性について説明してこの章を終わりにします。