トップページ > ミクロ経済学目次 > CES関数について 1 2 3 4
(2’)
初めに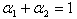 という制約を設けておく。
という制約を設けておく。
両辺に対数をとると
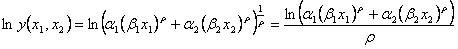
である。このとき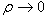 とすると
とすると
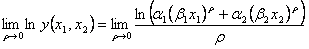
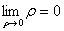
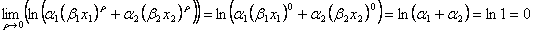
となり、 において不定形である。また、分子、分母のそれぞれの関数が連続微分可能であるのでロピタル・ルールが適用できる。したがって
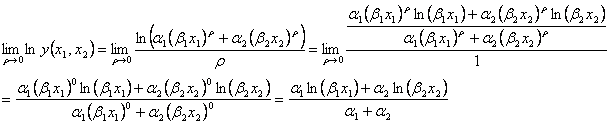
とおけば、
自然対数を両辺にとることは単調変換であるため、
である。これはコブ=ダグラス型関数である。尚、CES関数が1次同次であるため、ここで求められた関数もまた一次同次でなければならない。つまり、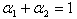 という制約は整合的であったのである。
という制約は整合的であったのである。
証了
(3’)
両辺に対数をとると
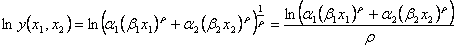
である。このとき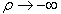 とすると
とすると
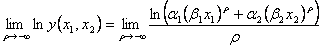
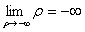
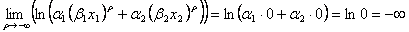
となり、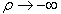 において不定形である。また、分子、分母のそれぞれの関数が連続微分可能であるのでロピタル・ルールが適用できる。したがって
において不定形である。また、分子、分母のそれぞれの関数が連続微分可能であるのでロピタル・ルールが適用できる。したがって
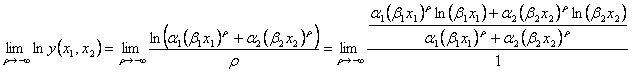
(i) 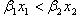 のとき、
のとき、
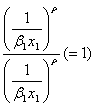
をかけると
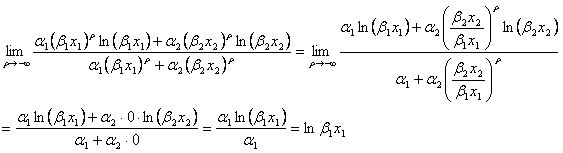
両辺に自然対数をとることは単調変換であるから、
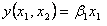
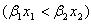
(ii) 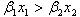 のとき、
のとき、
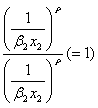
をかけると
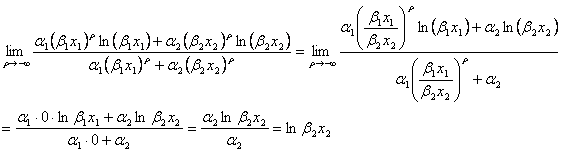
両辺に自然対数をとることは単調変換であるから、
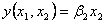
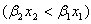
(iii) 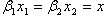 のとき、
のとき、
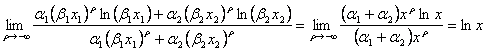
両辺に自然対数をとることは単調変換であるから、
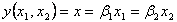
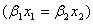
したがって、
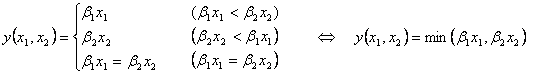
である。これは、レオンチェフ型関数である。
証了
したがって、より一般的なCES関数は
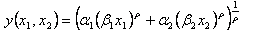
で表現することができる。n変数の時への一般化はまた時間があったらしますね。方法は上と変わらないと思いますし。

