トップページ > 経済数学目次 > 条件付き最適化問題 1 2 3
3.ラグランジェ未定乗数法続き
さきほどの例題が
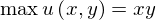
subject to 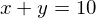
であるから、ラグランジェ関数を
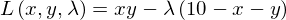
と定義します。(目的関数から制約式を=0の形にしてλをかけたものを引いた形です。)このラグランジェ関数を通常の最適化問題と同様にx,y,λについて偏微分して0とおきます。
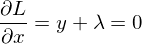
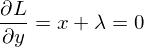
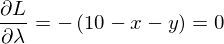
上記の上から1つ目と2つ目の式使ってλを消すと
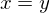
これを三つ目の式(制約式そのもの)に代入すると

と最適解が求まった。(ラグランジェ未定乗数の十分条件は縁付きヘッセの行列式で求めます。これは中級編で行うことにします。)
学部レベルで出てくる制約付き最適化問題は内点解になるよう調整されているものが多く、1階の条件で求めた解が2階の条件を満たしていることが多いです。また、関数が凹関数であるならば必ず内点解になり、2階の条件を満たしています。コブ=ダグラス型関数は必ず内点解になります。
線形だったり、レオンチェフ型だったり、すこし特殊な形で書かれている場合などは端点解になったり、最適値で微分不能だったりするので注意してください。私が今までに見た関数では
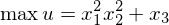
subject to 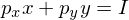
や
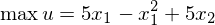
subject to 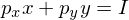
などが、パラメータの値によっては端点解になったり、内点解になったりしたちょっと複雑な問題としてありました。ですので、ちょっと注意して、ラグランジェ未定乗数法、または代入法を用いて解いてください。不安だったら、2階の条件で確かめることをお勧めします。
では、次のページではラグランジェ関数を最適化するのと同じようにラグランジェ関数を偏微分して=0とおいたものが、制約付き最適化条件の必要条件となっていることを証明します。そして最後に計算例をいくつか載せておきます。

