トップページ > 経済数学目次 > 微分入門 1 2 3 4 5 6 7 8
１．イントロダクション
経済学を学ぶ上で微分は必須です。しかし、逆を言えば、学部レベルの経済学を習得するには微分さえきちんとできれば、ほとんど問題ないといえます。（学部上級になると他にも必要になりますが。）ここでは、微分とは何かということから、積の微分、合成関数の微分、商の微分について説明しています。指数と対数の微分についてはこの章ではなく次の章で説明します。それでは、どうぞお聞きください★
２．微分はなにをしているのか？
微分するとは何をしているのか？それを簡単に述べれば、中学生の時に習った「平均の傾き」が「接線の傾き」とほぼ一致するところを求めるということです。
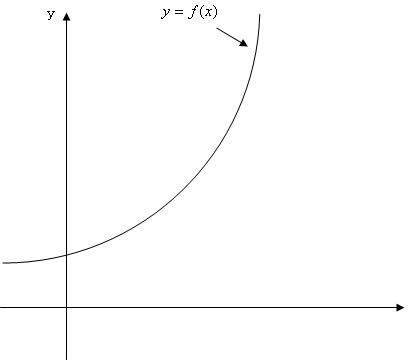
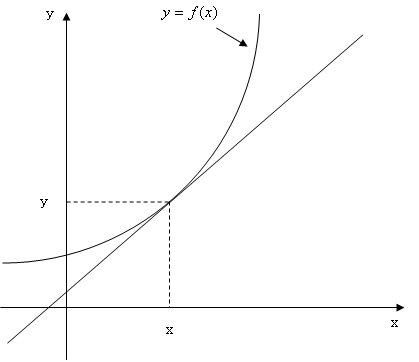
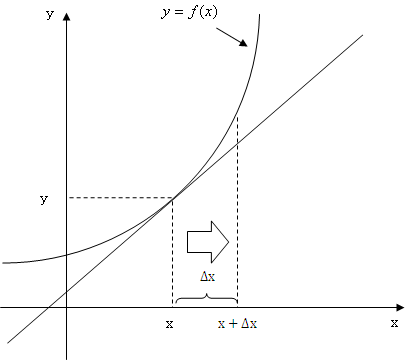
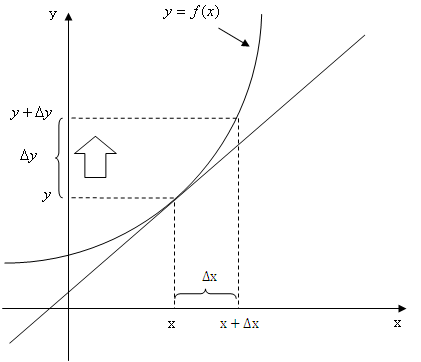
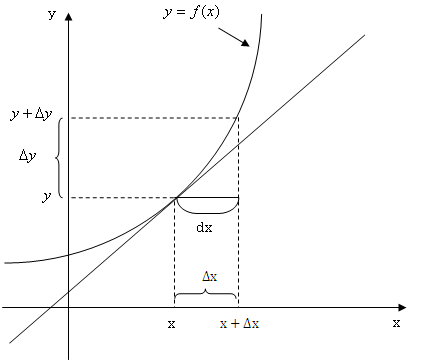
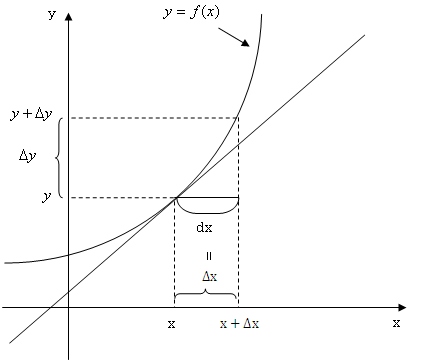
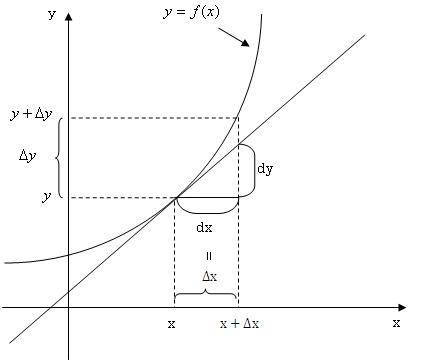
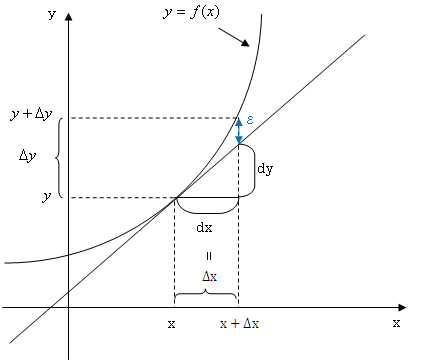
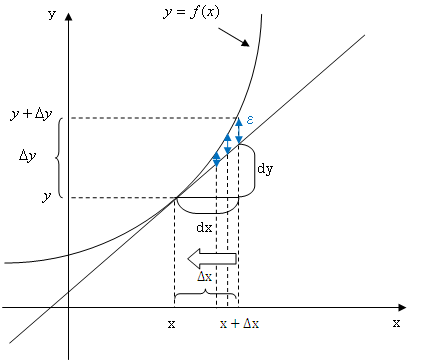
今、右の図のようなy=f(x)という曲線があります。そのとき、ある点（x,y）で接する接線を考えます。（右の図をクリック）平均の傾きは言葉で表すと、「ｙの増加分÷ｘの増加分」でしたね。前章で説明したようにｘの増加分（差分）はΔxで表せます。（右の図をクリック）（Δについてわからない方は変化率のページへ）?yはｘを増加させた時のyからの増加分です。（右の図をクリック）そうすると、平均の傾きは（Δy/Δx）で表せますね。次に接線までの増加分を考えます。記号を区別するためにΔではなく、ｄを使います。まず、ｘの接線までの増加分をdxとします。（右の図をクリック）これはΔxと同じ大きさにしておきます。（右の図をクリック）ｘが増加したときのｙの接線までの増加分をdyとします。（右の図をクリック）とするとΔxとdxは等しくしましたが、Δyとdyに違いがありますよね？その違いをε（＝Δy−dy）と表します。（右の図をクリック）そして、その誤差はΔxが小さくなればなるほど、その誤差εが小さくなるんです。（右の図をクリック）つまりΔxが０に近づくほどΔyとdyが等しくなっていくのです！Δxが０に近づくことを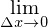
という記号で表せ、Δxとdxは等しく、Δxが０に近づけばΔyはdyと等しくなりますから、
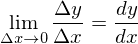
という式が成り立つということになります。左の式は「平均の傾き」をあらわしてますね？そして右の式は接線までのｙの増加分を接線までのｘの増加分で割ったものですから、「接線の傾き」を表してますね？これはつまり、Δxが０に近いところでは、「平均の傾き」が「接線の傾き」とほぼ等しくなっていることを示しているんですよ。そして、y=f(x)として、接線の傾きをf'(x)とすれば
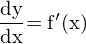
となります。
つまり「微分する」とは「接線の傾きf'(x)を求める」ということなのです。また、微分可能であるというのは関数のグラフがなめらかであるということなのです。ちなみにdyのことを「yの微分」と呼び、dxのことを「xの微分」と呼びます。ところでy＝3xなどの式で3のことをｘの係数と呼びますよね？上の式を書き換えると、dy=f'(x)dxとなりますから、f'(x)はdxの係数、dxはｘの微分ですから、f'(x)は微分係数と呼ばれるのです。だから「微分する」は「微分係数を求める」ということでもあります。また、点aにおいて微分するは微分係数f'(a)を求めることですが、y=f(x)を微分してy'=f'(x)を求めることを「導関数」を求めるともいいます。なぜかといいますと、y'=f'(x)は関数y=f(x)から導かれた（派生した,由来した）新しい関数と捉えられ、「導関数」(derivative)と呼ばれるからです。